Luca's meaningless thoughts  

After a small (but important) step towards making the D GC truly concurrent (which is my main goal), I've been exploring the possibility of making the mark phase recursive instead of iterative (as it currently is).

The motivation is that the iterative algorithm makes several passes through the entire heap (it doesn't need to do the full job on each pass, it processes only the newly reachable nodes found in the previous iteration, but to look for that new reachable node it does have to iterate over the entire heap). The number of passes is the same as the connectivity graph depth, the best case is where all the heap is reachable through the root set, and the worse is when the heap is a single linked list. The recursive algorithm, on the other hand, needs only a single pass but, of course, it has the problem of potentially consuming a lot of stack space (again, the recurse depth is the same as the connectivity graph depth), so it's not paradise either.

To see how much of a problem is the recurse depth in reality, first I've implemented a fully recursive algorithm, and I found it is a real problem, since I had segmentation faults because the (8MiB by default in Linux) stack overflows. So I've implemented an hybrid approach, setting a (configurable) maximum recurse depth for the marking phase. If the maximum depth is reached, the recursion is stopped and nodes that should be scanned deeply than that are queued to scanned in the next iteration.

Here are some results showing how the total run time is affected by the maximum recursion depth:

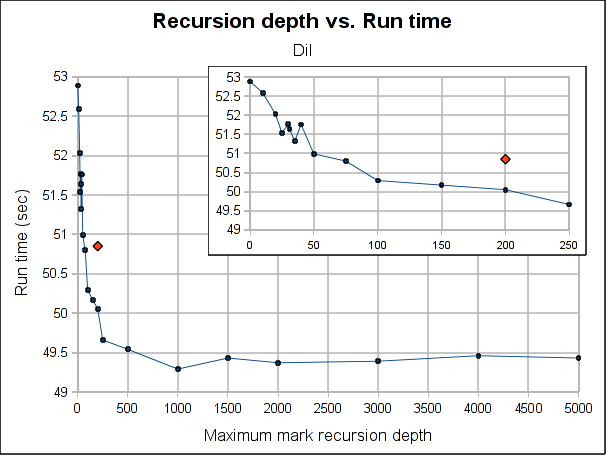
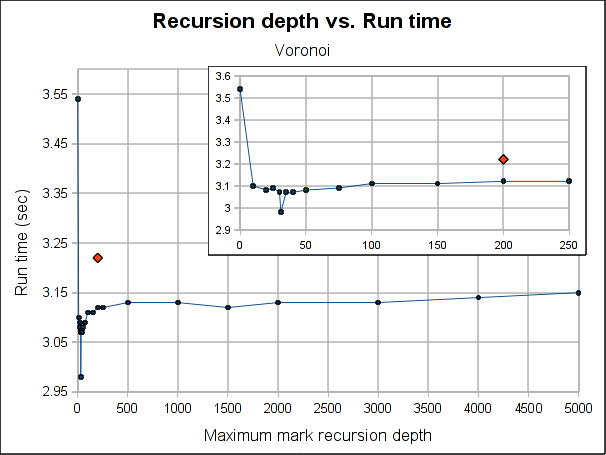
The red dot is how the pure iterative algorithm currently performs (it's placed arbitrarily in the plot, as the X-axis doesn't make sense for it).

The results are not very conclusive. Even when the hybrid approach performs better for both Dil and Voronoi when the maximum depth is bigger than 75, the better depth is program specific. Both have its worse case when depth is 0, which makes sense, because is paying the extra complexity of the hybrid algorithm with using its power. As soon as we leave the 0 depth, a big drop is seen, for Voronoi big enough to outperform the purely iterative algorithm, but not for Dil, which matches it near 60 and clearly outperforms it at 100.

As usual, Voronoi challenges all logic, as the best depth is 31 (it was a consistent result among several runs). Between 20 and 50 there is not much variation (except for the magic number 31) but when going beyond that, it worsen slowly but constantly as the depth is increased.

Note that the plots might make the performance improvement look a little bigger than it really is. The best case scenario the gain is 7.5% for Voronoi and 3% for Dil (which is probably better measure for the real world). If I had to choose a default, I'll probably go with 100 because is where both get a performance gain and is still a small enough number to ensure no segmentation faults due to stack exhaustion is caused (only) by the recursiveness of the mark phase (I guess a value of 1000 would be reasonable too, but I'm a little scared of causing inexplicable, magical, mystery segfaults to users). Anyway, for a value of 100, the performance gain is about 1% and 3.5% for Dil and Voronoi respectively.

So I'm not really sure if I should merge this change or not. In the best case scenarios (which requires a work from the user to search for the better depth for its program), the performance gain is not exactly huge and for a reasonable default value is so little that I'm not convinced the extra complexity of the change (because it makes the marking algorithm a little more complex) worth it.

Feel free to leave your opinion (I would even appreciate it if you do :).

In this post I will take a closer look at the Gcx.mark() and Gcx.fullcollect() functions.

This is a simplified version of the mark algorithm:

mark(from, to)
    changes = 0
    while from < to
        pool = findPool(from)
        offset = from - pool.baseAddr
        page_index = offset / PAGESIZE
        bin_size = pool.pagetable[page_index]
        bit_index = find_bit_index(bin_size, pool, offset)
        if not pool.mark.test(bit_index)
            pool.mark.set(bit_index)
            if not pool.noscan.test(bit_index)
                pool.scan.set(bit_index)
                changes = true
        from++
        anychanges |= changes // anychanges is global

In the original version, there are some optimizations and the find_bit_index() function doesn't exist (it does some bit masking to find the right bit index for the bit set). But everything else is pretty much the same.

So far, is evident that the algorithm don't mark the whole heap in one step, because it doesn't follow pointers. It just marks a consecutive chunk of memory, assuming that pointers can be at any place in that memory, as long as they are aligned (from increments in word-sized steps).

fullcollect() is the one in charge of following pointers, and marking chunks of memory. It does it in an iterative way (that's why mark() informs about anychanges (when new pointer should be followed to mark them, or, speaking in the tri-colour abstraction, when grey cells are found).

fullcollect() is huge, so I'll split it up in smaller pieces for the sake of clarity. Let's see what are the basic blocks (see the second part of this series):

fullcollect()
    thread_suspendAll()
    clear_mark_bits()
    mark_free_list()
    rt_scanStaticData(mark)
    thread_scanAll(mark, stackTop)
    mark_root_set()
    mark_heap()
    thread_resumeAll()
    sweep()

Generaly speaking, all the functions that have some CamelCasing are real functions and the ones that are all_lowercase and made up by me.

Let's see each function.

thread_suspendAll()

This is part of the threads runtime (found in src/common/core/thread.d). A simple peak at it shows it uses SIGUSR1 to stop the thread. When the signal is caught it pushes all the registers into the stack to be sure any pointers there are scanned in the future. The threads waits for SIGUSR2 to resume.

clear_mark_bits()

foreach pool in pooltable
    pool.mark.zero()
    pool.scan.zero()
    pool.freebits.zero()

mark_free_list()

foreach n in B_16 .. B_PAGE
    foreach node in bucket
        pool = findPool(node)
        pool.freebits.set(find_bit_index(pool, node))
        pool.mark.set(find_bit_index(pool, node))

rt_scanStaticData(mark)

This function, as the name suggests, uses the provided mark function callback to scan the program's static data.

thread_scanAll(mark, stackTop)

This is another threads runtime function, used to mark the suspended threads stacks. I does some calculation about the stack bottom and top, and calls mark(bottom, top), so at this point we have marked all reachable memory from the stack(s).

mark_root_set()

mark(roots, roots + nroots)
foreach range in ranges
    mark(range.pbot, range.ptop)

mark_heap()

This is where most of the marking work is done. The code is really ugly, very hard to read (mainly because of bad variable names) but what it does it's relatively simple, here is the simplified algorithm:

// anychanges is global and was set by the mark()ing of the
// stacks and root set
while anychanges
    anychanges = 0
    foreach pool in pooltable
        foreach bit_pos in pool.scan
            if not pool.scan.test(bit_pos)
                continue
            pool.scan.clear(bit_pos) // mark as already scanned
            bin_size = find_bin_for_bit(pool, bit_pos)
            bin_base_addr = find_base_addr_for_bit(pool, bit_pos)
            if bin_size < B_PAGE // small object
                bin_top_addr = bin_base_addr + bin_size
            else if bin_size in [B_PAGE, B_PAGEPLUS] // big object
                page_num = (bin_base_addr - pool.baseAddr) / PAGESIZE
                if bin == B_PAGEPLUS // search for the base page
                    while pool.pagetable[page_num - 1] != B_PAGE
                        page_num--
                n_pages = 1
                while page_num + n_pages < pool.ncommitted
                        and pool.pagetable[page_num + n_pages] == B_PAGEPLUS
                    n_pages++
                bin_top_addr = bin_base_addr + n_pages * PAGESIZE
            mark(bin_base_addr, bin_top_addr)

The original algorithm has some optimizations for proccessing bits in clusters (skips groups of bins without the scan bit) and some kind-of bugs too.

Again, the functions in all_lower_case don't really exist, some pointer arithmetics are done in place for finding those values.

Note that the pools are iterated over and over again until there are no unvisited bins. I guess this is a fair price to pay for not having a mark stack (but I'm not really sure =).

thread_resumeAll()

This is, again, part of the threads runtime and resume all the paused threads by signaling a SIGUSR2 to them.

sweep()

mark_unmarked_free()
rebuild_free_list()

mark_unmarked_free()

This (invented) function looks for unmarked bins and set the freebits bit on them if they are small objects (bin size smaller than B_PAGE) or mark the entire page as free (B_FREE) in case of large objects.

This step is in charge of executing destructors too (through rt_finalize() the runtime function).

rebuild_free_list()

This (also invented) function first clear the free list (bucket) and then rebuild it using the information collected in the previous step.

As usual, only bins with size smaller than B_PAGE are linked to the free list, except if the pages they belong to have all the bins freed, in which case the page is marked with the special B_FREE bin size. The same goes for big objects freed in the previous step.

I think rebuilding the whole free list is not necessary, the new free bins could be just linked to the existing free list. I guess this step exists to help reducing fragmentation, since the rebuilt free list group bins belonging to the same page together.