Luca's meaningless thoughts  

Python (at least CPython) uses reference counting, and since version 2.0 it includes a cycles freeing algorithm. It uses a generational approach, with 3 generations.

Python makes a distinction between atoms (strings and numbers mostly), which can't be part of cycles; and containers (tuples, lists, dictionaries, instances, classes, etc.), which can. Since it's unable to find all the roots, it keeps track of all the container objects (as a double linked list) and periodically look in them for cycles. If somebody survive the collection, is promoted to the next generation.

I think this works pretty well in real life programs (I never had problems with Python's GC -long pauses or such-, and I never heard complains either), and I don't see why it shouldn't work for D. Even more, Python have an issue with finalizers which don't exist in D because you don't have any warranties about finalization order in D already (and nobody seems to care, because when you need to have some order of finalization you should probably use some kind of RAII).

This is a more polished version of the last idea about adding a backup tracing GC to collect cycles. We just trace the areas of the heap that can potentially store cycles (instead of tracing all the heap).

So, how do we know which areas may have cycles? When a reference counter is decremented, if it becomes zero, it can't possibly part of a cycle, but when the counter is decremented 1 or more, you never know. So the basics for the algorithm is to store cells which counters have been decremented to 1 or more, and then make a local (partial) mark and sweep to the cell accessible from it.

The trick is to use the reference counters. In the marking phase, the reference counters are decremented as the connectivity graph is traversed. When the marking phase is done, any cell with counter higher than zero is reference from outside the partial graph analyzed, so it must survive (as well as all the cells reachable from it).

There are a lot of flavors of this algorithm, but all are based on the same principle, and most of the could be suitable for D.

The simpler way to reclaim cycles is to use a backup tracing garbage collector. But this way, even when GC frequency could be much lower, the infomation of reference counters are not used, and pauses can be very long (depending on the backup algorithm used).

I think some kind of mixture between RC and tracing GC could be done so I wont discard this option just yet, but I think more specialized algorithms can do better in this case.

Finally, we address the cyclic structures reclaimation when doing reference counting. But I think there are some algorithms that are clearly unsuitable for D.

All the manual techniques (manually avoiding or breaking cycles or using weak pointers) are unacceptable, because it throws the problem again to the programmer. So I will consider only the options that keep the memory management automatic.

There are several specific cycles reclamation algorithms for functional languages too (like Friedman and Wise), but of course they are unsuitable for D because of the asumptios they make.

Bobrow proposed a general technique, in which a cyclic structure is reference counted as a whole (instead of reference counting their individual cells) but I find this impractical for D too, because it needs programmer intervention (marking "group" of cells).

There's not much to think about it (I think ;).

ZCT doesn't help in cycles reclaiming, because ZCT tracks cells with zero count, and cycles can't possibly have a zero count (even using deferred reference counting), because they are, by definition, inter-heap pointers.

Let's see a simple example:

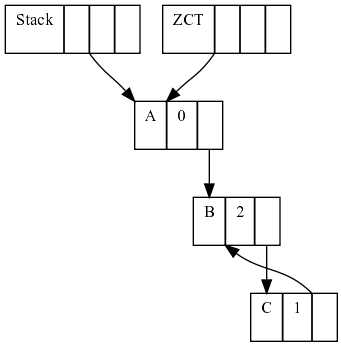
First, we have 3 heap cells, A pointed only by the (thus with rc 0 and added to the ZCT) and B pointed by A and in a cycle with C.

If sometime later, A stop pointing to B, the cycle B-C is not pointed by anything (the ZCT can't do anything about it either), so we lost track of the cycle.

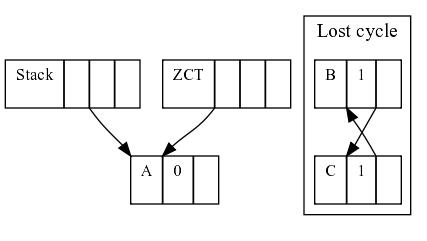
Does this mean that deferred reference counting is useless? I think not. It could still be useful to do some kind of incremental garbage collection, minimizing pauses for a lot of cases. As long as the ZCT reconciliation can find free cells, the pauses of GC would be as short as tracing only the stack, which I think it would be pretty short.

If the ZCT reconciliation can't find free cells, a full collection should be triggered, using a tracing collector to inspect both the stack and the heap. Alternatively, one can a potential cycle table to store cells which rc has been decremented to a value higher than zero, and then just trace those cells to look for cycles, but we will see this algorithm in more detail in the future.